Thevenin’s Theorem: A Beginner’s Guide

                              
 

table of content 

1. Introduction
2. History of Thevenin’s theorem
3. Basic circuit analysis concepts
4. Voltage, current, and resistance
5. Ohm’s law
6. Thevenin’s theorem: principles and applications
7. Statement of the theorem
8. Finding the Thevenin equivalent circuit
9. What is Thevenin’s theorem?
10. When should you use Thevenin’s theorem?
11. How do you apply Thevenin’s theorem to a circuit
12. Conclusion.

Introduction

Electrical engineers can effectively convert complicated circuits into smaller equivalent circuits by using Thevenin's theorem. The French telegraph engineer Léon Charles Thévenin is honored by having his theorem called in his honor. He proposed it in 1883.

History of Thevenin’s theorem

Hermann von Helmholtz, a German scientist, independently derived Thevenin's theorem in 1853; Léon Charles Thévenin did the same in 1883. Although it was initially solely intended to apply to direct-current resistive circuits, it has recently been expanded to include AC circuits.

Basic circuit analysis concepts

Finding the voltages and currents in each component of an electrical circuit is the process of circuit analysis. The goal of this is to use a proven set of equations to resolve issues in electric circuits. The node voltage approach and mesh current method are two well-liked techniques for circuit analysis.

Voltage, current, and resistance

In electrical engineering, three essential quantities are voltage, current, and resistance. Current is the pace at which charge is flowing, resistance is a material's propensity to oppose the flow of charge (current), and voltage is the difference in charge between two places. Ohm's Law, which states that the voltage across a conductor is directly proportional to the current flowing through it, relates these three values.

Ohm’s law

Under the assumption that all physical parameters and temperatures remain constant, Ohm's Law asserts that the voltage across a conductor is directly proportional to the current flowing through it. V = IR, where V is the voltage across the conductor, I is the current flowing through the conductor, and R is the conductor's resistance, is a mathematical expression for this relationship.

Thevenin’s theorem: principles and applications

According to Thevenin's Theorem, any linear circuit with multiple voltage sources and resistors may be reduced to a simpler version that just has one voltage source connected in series with a load. Any one-port network may be reduced using this theorem to a single voltage source and a single impedance. It can be used to examine a circuit's initial-condition and steady-state response as well as to simplify circuit analysis.

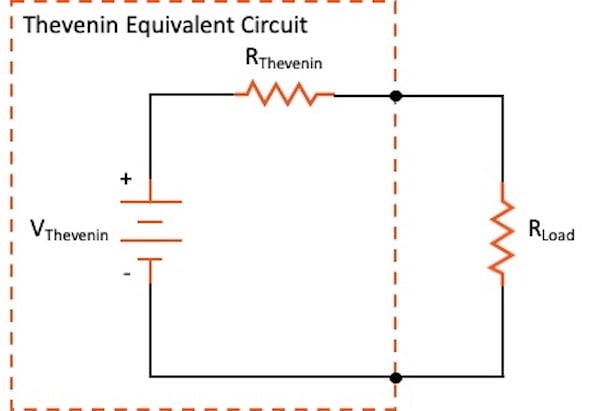
Statement of the theorem

"Any linear electrical network containing only voltage sources, current sources, and resistances can be replaced at terminals A to B by an equivalent combination of a voltage source Vth in series connection with a resistance Rth," states Thevenin's Theorem.

Finding the Thevenin equivalent circuit

We must first take the load resistance out of the original circuit in order to determine the Thevenin equivalent circuit. The equivalent resistance (Rth) of the circuit is then determined by opening all current sources and shorting all voltage sources. Finally, using standard circuit analysis, we discover Vth.

What is Thevenin’s theorem?

Thevenin's theorem, to put it simply, is a strategy for simplifying the comprehension and analysis of a challenging circuit. It accomplishes this by substituting a simple circuit component with just two other parts: a voltage source and a resistor. This is especially useful if you want to observe how the circuit reacts when the load (the component of the circuit that consumes power) is changed.

When should you use Thevenin’s theorem?

When examining the behavior of a circuit with a fluctuating load, Thevenin's theorem can be especially helpful. The overall resistance of the parallel connections in power systems, for instance, is dependent on how many loads are connected at once and how frequently they are switched on and off. By temporarily removing the load resistance from the original circuit and reducing what is left to an analogous circuit made up of a single voltage source and series resistance in such circumstances, Thevenin's theorem can greatly simplify the analysis. After reconnecting the load resistance to the Thevenin equivalent circuit, calculations can be performed as if the entire network were just a straightforward series circuit.

In summary, you may choose to use Thevenin’s theorem when analyzing a circuit with a changing load or when you want to simplify the analysis of a complex circuit. However, it is important to note that Thevenin’s theorem is only applicable to linear circuits containing only voltage sources, current sources, and resistances or impedances.

How do you apply Thevenin’s theorem to a circuit?

The load that you want to examine must be identified before you can apply Thevenin's theorem to a circuit. Once you've located the load, you can momentarily take it out of the circuit. The Thevenin equivalent voltage and resistance can then be determined using the circuit's remaining component. The open-circuit voltage across the terminals of the original circuit is known as the Thevenin equivalent voltage, and the resistance seen entering the original circuit from the terminals after all independent sources have been disconnected is known as the Thevenin equivalent resistance.

You can build a Thevenin equivalent circuit by connecting a voltage source with a value equal to the Thevenin equivalent voltage in series with a resistor with a value equal to the Thevenin equivalent resistance once you have determined the Thevenin equivalent voltage and resistance. By connecting the load across the voltage source's terminals, you can finally reattach it to the Thevenin equivalent circuit.

In order to apply Thevenin's theorem to a circuit, the load must first be identified and momentarily removed. Then, the Thevenin equivalent voltage and resistance must be discovered, along with a Thevenin equivalent circuit must be built using these values. Finally, the load must be reconnected to the Thevenin equivalent circuit.

We trust that this article has clarified what Thevenin's theorem is and how it can be applied to make circuit analysis easier. You may make even complex circuits simpler to comprehend and evaluate by using this effective technique.

 

Conclusion

Finally, Thevenin's theorem is a very helpful tool for converting complicated circuits into an equivalent circuit that consists of a single voltage source coupled in series with a load. Electrical engineers frequently apply this theorem to streamline and improve circuit analysis.

An effective technique for streamlining electrical circuit analysis is Thevenin's theorem. The purpose of this article was to explain Thevenin's theorem, when to apply it, and how it helps simplify circuit analysis.

Drop your questions in the comments.